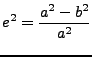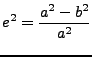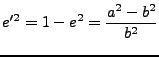


Next: Bibliography
Up: GEOCODE
Previous: Output Description
Contents
Known are the heights of each pixel in the master (line,pixel) system.
The point P(x,y,z) corresponding to a (line,pixel) is computed with
the 3 equations (see Annex D) in such a way that
it lies on an ellipsoid of height h above the refernce ellipsoid.
When these coordinates are known, the equations of Bowring are used to
transform them to an ellipsoid system
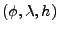 . The
semimajor axis is denoted by a, and the semiminor axis is
denoted by b. The squared first eccentricity by:
. The
semimajor axis is denoted by a, and the semiminor axis is
denoted by b. The squared first eccentricity by:
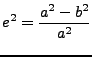 |
(1) |
The squared second eccentricity by
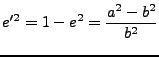 |
(2) |
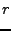 |
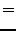 |
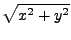 |
(3) |
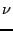 |
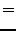 |
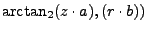 |
(4) |
 |
 |
 |
(5) |
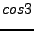 |
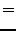 |
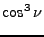 |
(6) |
| |
|
|
|
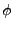 |
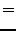 |
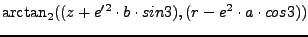 |
(7) |
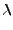 |
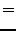 |
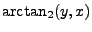 |
(8) |
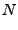 |
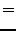 |
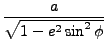 |
(9) |
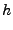 |
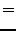 |
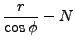 |
(10) |



Next: Bibliography
Up: GEOCODE
Previous: Output Description
Contents
Leijen
2009-04-14