2.1 Coxeter graphs

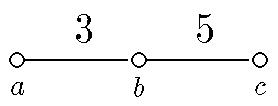
Each node x of a Coxeter graph specifies a generator x and the relation 1=x². If two distinct nodes x,y in a Coxeter graph are joined by an edge with label m where m is a positive integer, then this denotes the relation 1=(xy)^m. All the edges in our Coxeter graphs are labelled. If two distinct nodes x,y in a Coxeter graph are not joined by an edge, then this denotes the relation 1=(xy)². We specify a Coxeter graph C by a set of paths in C, each containing at least one edge, and which together contain all the edges of C. A typical path is of the form xmynz..., which means that x is joined to y with an edge labelled m y is joined to z with an edge labelled n and so on.

For example, the graph specified by the two paths a3b3c3d3a3c,b3d is the complete graph on a,b,c,d with all edge-labels 3. The Coxeter graph

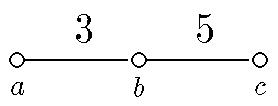
is denoted by a3b5c, which also denotes the presentation < a,b,c| 1=a²=b²=c²=(ab)³=(bc)⁵=(ac)² >

for 2xA₅. Note that we demand a Coxeter graph to have at least one edge.