

FpGroupViaStrings( cox )
FpGroupViaStrings( cox, relstring )
FpGroupViaStrings( cox, genstring, relstring )
FpGroupViaStrings( genstring, relstring )
FpGroupViaStrings( ... , extrarelstring )
FpGroupViaStrings( [ ... ] )
FpGroupViaStrings returns the finitely presented group generated by the generators present in cox and/or in genstring, and subject to the relations defined by cox and/or by relstring.
The Coxeter graph cox is expected to be represented as a string where every part between commas corresponds to a path in the Coxeter graph in the obvious way: for example, the graph specified by the two paths a3b3c3d3a3c,b3d should be represented as
gap> cox := "a3b3c3d3a3c,b3d";;
Generators can be given only by single capital or small letters. A small letter denotes a different generator from a capital letter. This limits the number of different generators that can be used in a string presentation to 52. When all relations are present in the Coxeter graph one can build the corresponding group:
gap> 2dira5 := FpGroupViaStrings( "K3L5M" );
## The map is: "KLM"
Group( f.1, f.2, f.3 )
gap> 2dira5.relators;
[ f.1*f.2*f.1*f.2*f.1*f.2, f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3,
f.1^2, f.2^2, f.3^2, f.1*f.3*f.1*f.3 ]
Besides of creating and returning the group, FpGroupViaStrings will print out a message that indicates how the string generators correspond with the generators of the finitely presented group. The first string generator found while analyzing the string presentation will correspond with the first generator of the finitely presented group, etcetera. This map has to be used for building subgroups via strings, see section 2.3. When generators are entered in a different order this will only result in a relabeling of the underlying generators used by GAP.
Generators can also be introduced in an explicit way: a string of letters like "a,b,c" will be interpreted as a list of generators. Note that for generators introduced in this way it is necessary to enter explicitly an order relation, as nothing will be assumed about the order of a generator.
gap> gen := "K,L,M";
"K,L,M"
gap> rel := "K^2,L^2,M^2,(KL)^3,(LM)^5,(KM)^2";
"K^2,L^2,M^2,(KL)^3,(LM)^5,(KM)^2"
gap> alt2dira5 := FpGroupViaStrings( gen, rel );
## The map is: "KLM"
Group( f.1, f.2, f.3 )
gap> alt2dira5.relators;
[ f.1^2, f.2^2, f.3^2, f.1*f.2*f.1*f.2*f.1*f.2,
f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3, f.1*f.3*f.1*f.3 ]
Relations should be presented as a string. Within the string, relations are separated by commas. A relation should be presented as a word in capital or small letters of the Latin alphabet. Besides letters the symbols ^, (, ) and = will be recognised. So, for example blanks and commutator signs are not recognised yet and may cause error messages. The symbol ^ stands for the power operation when the right hand side is a number and for conjugation when the right hand represents a word. Symbols should be grouped using normal brackets (.). Single symbols do not need to be grouped. Some examples :
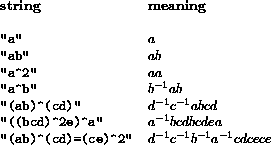
A list of strings that, besides the normal relations, contains the string _PCE will be recognised as a list of relations that are not necessary to define the group in question but are meant to speed up a Coset Enumeration process. Whether these relations will be added to the group relations during the construction of the Group Record, is dependent on the value of the global boolean variable GPL_PCE. Here _PCE stands for Purpose of Coset Enumeration. For example:
gap> cox := "a3b5c3d3e4c";; rel := "a=(ce)^2";; gap> extrarel := "_PCE,(abc)^5,(bcd)^5"; "_PCE,(abc)^5,(bcd)^5" gap> m11 := FpGroupViaStrings( cox, rel, extrarel );; && The map is: "abcde" gap> m11.relators; [ f.1*f.2*f.1*f.2*f.1*f.2, f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3, f.3*f.4*f.3*f.4*f.3*f.4, f.4*f.5*f.4*f.5*f.4*f.5, f.5*f.3*f.5*f.3*f.5*f.3*f.5*f.3, f.1^2, f.2^2, f.3^2, f.4^2, f.5^2, f.1*f.3*f.1*f.3, f.1*f.4*f.1*f.4, f.1*f.5*f.1*f.5, f.2*f.4*f.2*f.4, f.2*f.5*f.2*f.5, f.1^-1*f.3*f.5*f.3*f.5, f.1*f.2*f.3*f.1*f.2*f.3*f.1*f.2*f.3*f.1*f.2*f.3*f.1*f.2*f.3, f.2*f.3*f.4*f.2*f.3*f.4*f.2*f.3*f.4*f.2*f.3*f.4*f.2*f.3*f.4 ] gap> GPL_PCE := false;; gap> m11 := FpGroupViaStrings( cox, rel, extrarel );; && The map is: "abcde" gap> m11.relators; [ f.1*f.2*f.1*f.2*f.1*f.2, f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3*f.2*f.3, f.3*f.4*f.3*f.4*f.3*f.4, f.4*f.5*f.4*f.5*f.4*f.5, f.5*f.3*f.5*f.3*f.5*f.3*f.5*f.3, f.1^2, f.2^2, f.3^2, f.4^2, f.5^2, f.1*f.3*f.1*f.3, f.1*f.4*f.1*f.4, f.1*f.5*f.1*f.5, f.2*f.4*f.2*f.4, f.2*f.5*f.2*f.5, f.1^-1*f.3*f.5*f.3*f.5 ]
FpGroupViaStrings will also accept a list containing entries as described above.
gap> list := [cox, rel, extrarel];; gap> Size( FpGroupViaStrings( list )); && The map is: "abcde" 7920