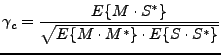 |
(1) |
In this step the following is computed. The (complex) coherence image is computed, with or without subtraction of the reference phase and the radarcoded DEM phase. The reference phase is subtracted if there is a 2d-polynomial in the products result file (result of step FLATEARTH). It is not subtracted if this is not in the result file or if the number of coefficients is set to 0. For a proper estimation of the coherence map, especially over mountainous areas, the radarcoded DEM phase should also be subtracted. In this case, the result of step COMPREFDEM is required in the products result file. This is the default procedure since v4.01.
The complex coherence image between two images is defined as:
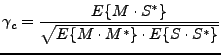 |
(1) |
The coherence is defined by
![]() and its estimator as:
and its estimator as:
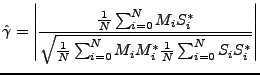 |
(2) |
Data buffering is applied for the memory considerations.