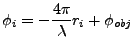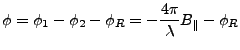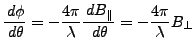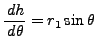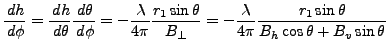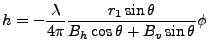


Next: Method rodriguez
Up: Implementation
Previous: Implementation
Contents
This method yields first the heights of the (line,pixel) and the
position P(x,y,z). In this manner the geocoding can be done in the
same step. by converting P(x,y,z) (known h) to phi,lambda. If there
is a trend in the height this has to be removed first, e.g. by using
tiepoints. This means the computed phi and lambda matrices are not
correct anymore.
With the baseline defined as in Annex D the
following equations hold.
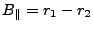 |
(1) |
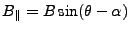 |
(2) |
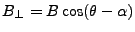 |
(3) |
Note the sign, must be minus.
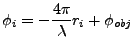 |
(4) |
Content of unwrapped interferogram (never mind the -phiR).
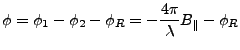 |
(5) |
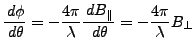 |
(6) |
Geometric equation:
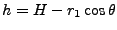 |
(7) |
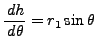 |
(8) |
Height ambiguity:
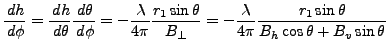 |
(9) |
Final equation to convert phase to height:
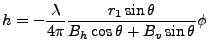 |
(10) |
The procedure to compute the height is as follows (note that
computation is skipped if unwrapping went wrong, indicated by NaN (not
a number) in the unwrapped interferogram.)
- for all lines
- .i1. compute
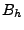 and
and 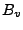 (by computing h for middle pixel,
then compute baseline).
(by computing h for middle pixel,
then compute baseline).
- .i2. hcurrent = 0
- for all pixels
- .j1. if value unwrapped phase equals NaN
 -999 then
goto next pixel
-999 then
goto next pixel
- .j2. compute
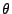 (corresponding to h)
(corresponding to h)
- .j3. hlast=hcurrent, compute hcurrent with formula
- if ((hlast - hcurrent )
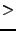 k) then goto .j2.
k) then goto .j2.



Next: Method rodriguez
Up: Implementation
Previous: Implementation
Contents
Leijen
2009-04-14