Use same definitions as exact method, see also
Annex D. See also [12]. This
method uses the geometry to compute
![]() . There are
two errors in it for now. First H is not computed exact. Second the
baseline parameters are not computed exact per line. P is evaluated
at reference surface and S according to that position. This means
that if the orbits are not parallel the point S is not computed
correctly, which introduces errors in the baseline computation.
The co-registration model is better used for that.
. There are
two errors in it for now. First H is not computed exact. Second the
baseline parameters are not computed exact per line. P is evaluated
at reference surface and S according to that position. This means
that if the orbits are not parallel the point S is not computed
correctly, which introduces errors in the baseline computation.
The co-registration model is better used for that.
Known:
r1 range to M,P
position M
B baseline
![]() baseline orientation with regard to (equals our def. of alpha)
baseline orientation with regard to (equals our def. of alpha)
Compute:
theta (angle state, look: with formulas exact (no iterations)
H height sat above some surface ?? how to compute this exact??
The following we derived for our baseline definition: (beta = angle (2-1,P-1) counterclockwise:)
| (11) |
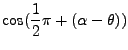 |
(12) | ||
| (13) |
| (14) |
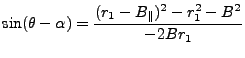 |
(15) |
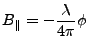 |
(16) |
 |
(17) |
| (18) |
Compute H from known: theta, position Master (rho1), r1 In triangle (1,P,0) three Start with cosine law for line across theta = p
| (19) |
| (20) |
| (21) |
| (22) |
This will cause a bias and some trend in the height. Because there likely already is a trend due to orbit errors, this is not as bad as it might seem. By using tie points a good height may be computed. For now we did not implement a routine that uses tie points.
New way of computing H: (NOT implemented, to difficult)
Problems with this method: how do you know orientation of theta? rotation of ellips to new system.
A few more notes:
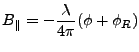 |
(23) |
Processing:
The idea is to compute H from the position of M. (H can be computed by (reference needed) as shown.) And then to find theta=f(B,phi,r). And then find h with the first equation. This method is implemented to check our exact method, the results are very different.
In this method the point P does not have to be computed. (though in order to compute baseline components we will compute a point P on height h (evaluate, iteratively) once for every line.)
A better way might be to use the co-registration model to compute the point S.