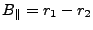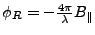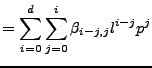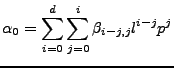


Next: Comparison of the methods
Up: Implementation
Previous: Method rodriguez
Contents
This method is described in [15]. It is a fast method
that yields the radar coded heights. It is based on the idea to first
compute the reference fase at a number of heights and then to compare
the actual phase from the interferogram with these values to determine
the height.
A problem is that the interferogram does not contain the reference
phase anymore, so that has to be added to the estimated phi.
It uses a number of steps which are described below.
- Compute reference phase at a NL locations (line,pixel)
at NH (=3) heights (0, 2000 and 4000m).
for h=0, 2000, 4000:
- ellips.a=wgs84.a+h, ellips.b=wgs84.b+h
- compute position of master satellite, corresponding point P on
ellips and position of slave satellite, see annex
D.
-
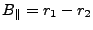
-
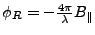
- store the values and locations and heights.
Note that the
reference phase defined like this typically is something like 5000
(rad) even for h=0. Therefor the reference phase for h=0 is set to
0, (because in the unwrapped interferogram the reference phase is
removed, if the phase of the unwrapped interferogram is 0, then this
should yield a height of 0) and the reference phase for height h is
set to refphaseh - refphase0. (This makes the computations as done
later a little stupid, to estimate coefficients which are by
definition equal to 0.) (An other possibility is not to do this
here, but later when the functions are evaluated to add the
reference phase to each pixel. I have tested this and the results
are identical (+- .4m))
- Compute for each location a polynomial (1d degree 1dD (= NH-1))
to describe
the height as a function of reference phase at these points.
For each location it holds ( for height i):
for height i):
So it is easy to solve (exact) for 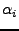 per location.
per location.
- Compute (1dD+1=NH) polynomials to describe the coefficients of
the previous step as a function of location. (now, for a random
location, the coefficients of height as a function of the reference
phase can be computed.) For example for
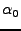 computed at NL
locations (l,p) a 2d polynomial can be used:
computed at NL
locations (l,p) a 2d polynomial can be used:
A linear system can be easily set up and solved (least squares) by
cholesky factorization. A rescaling needs to be applied to avoid
instability. The system can be solved simultaneously for all
alphas, because the normal matrix (and factorization) remains the
same, but somehow our cholesky routine introduced an error (which is
probably caused by using fortran in c) so we just solve 3 seperate
times with the same factored normalmatrix.
- Evaluate for all points at (line,pixel) with ok unwrapped phase
the 2d polynomial to obtain the coefficients of the height(phi)
function.
Then evaluate the 1d polynomial to obtain the height.
For all (l,p) with ok unwrapped phase:
- Compute the alphas.
For betas appropriate to alpha0:
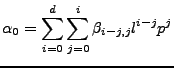 |
(28) |
- For betas appropriate to alpha1:
 |
(29) |
- repeat computing alphas until you have them all (1dD+1).
- Compute the height.
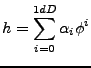 |
(30) |



Next: Comparison of the methods
Up: Implementation
Previous: Method rodriguez
Contents
Leijen
2009-04-14