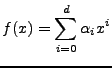Polynomials

A 1d-polynomial is defined as:

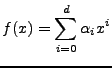$$f(x) = \sum_{i=0}^{d} \alpha_{i} x^{i}$$ (D25)

A 2d-polynomial is defined as:

$$f(x,y) = \sum_{i=0}^{d}\sum_{j=0}^{i} \alpha_{i-j, j} x^{i-j} y^{j}$$ (D26)

Thus the order of the coefficients (line,pixel) is independent of degree d:
d=0: $A_{00}$ (1)
d=1: $A_{10} A_{01}$ (2, 3)
d=2: $A_{20} A_{11} A_{02}$ (4, 5, 6)
d=3: $A_{30} A_{21} A_{12} A_{03}$ (7, 8, 9, 10)

Thus the number of coefficients (unknowns in least squares estimation) equals for a 2d-polynomial of degree d:

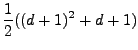$$\ensuremath{{1\over2}}((d+1)^{2}+d+1)$$ (D27)

And the degree of a polynomial with N coefficients is equal to:

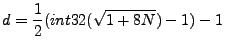$$d = \ensuremath{{1\over2}}(int32(\sqrt{1 + 8N}) - 1) - 1$$ (D28)