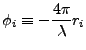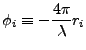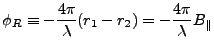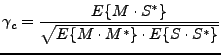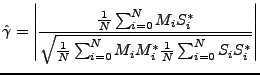


Next: Polynomials
Up: Definitions
Previous: Baseline
Contents
Interferogram
The phase for a certain pixel in a single SLC image i is defined as:
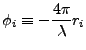 |
(D14) |
The complex interferogram minus reference phase is defined as:
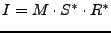 |
(D15) |
Where:
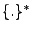 denotes the complex conjugated;
denotes the complex conjugated;
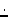 denotes a pointwise multiplication;
denotes a pointwise multiplication;
I is the complex interferogram;
M is the complex master image;
S is the complex (resampled) slave image;
R is the complex (amplitude  1) reference phase;
1) reference phase;
The phase image (of complex interferogram minus reference phase) is
defined as:
 |
(D16) |
Where:
 is the four quadrant arc tangent;
is the four quadrant arc tangent;
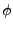 is the phase image;
is the phase image;
I is the complex interferogram;
Which is equal to (with an ambiguity of 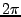 )
)
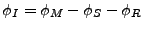 |
(D17) |
The reference phase is defined as (where 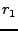 denotes the range from
the master satellite to a point on the reference surface)
denotes the range from
the master satellite to a point on the reference surface)
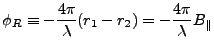 |
(D18) |
Which is the same as
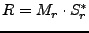 |
(D19) |
Where 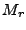 denotes the phase of a point situated on the reference
surface. (of course, in this definition the phase of the
interferogram equals zero if there actually is no topography (and
denotes the phase of a point situated on the reference
surface. (of course, in this definition the phase of the
interferogram equals zero if there actually is no topography (and
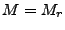 ).) The values of the (real valued) reference phase are stored
in a 2d-polynomial of certain degree. The subtraction of the
reference phase
).) The values of the (real valued) reference phase are stored
in a 2d-polynomial of certain degree. The subtraction of the
reference phase 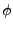 is actually computed as:
is actually computed as:
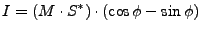 |
(D20) |
because the complex conjugated of the reference phase 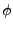 equals:
equals:
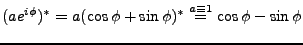 |
(D21) |
The complex coherence between two images is defined as (see [18]):
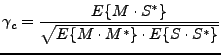 |
(D22) |
Where:
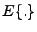 is the expectation;
is the expectation;
 is the complex conjugated;
is the complex conjugated;
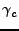 is the complex coherence;
is the complex coherence;
M is the complex master image;
S is the complex slave image
(possibly minus (complex) reference phase:
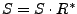 ;
;
The coherence is defined by
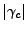 , and its estimator as:
, and its estimator as:
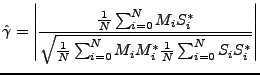 |
(D23) |
The correlation between two images is defined by (see [2]):
 |
(D24) |
Thus the mean is first subtracted in comparison to the coherence. The
coherence is equal to the correlation only if
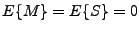 .
.
A problem is that the estimator for the coherence and correlation is
biased. For small window sizes its outcome is too high. This
probably also causes the problems in the coarse coregistration, where
the most likely offset is not selected based on its correlation value
but on its consistency.



Next: Polynomials
Up: Definitions
Previous: Baseline
Contents
Leijen
2009-04-14