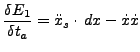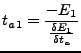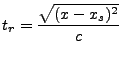


Next: Orbit interpolation
Up: Definitions
Previous: pixel number
Contents
Doppler, range and ellipsoid equations
The following three equations are used regularly throughout the
software to compute the point P that corresponds to a certain line and
pixel in the master or slave image (see also [7]).
Precise orbits are necessary.
- Doppler: The point P at the surface lies perpendicular to the orbit
due to zero Doppler processing
(otherwise this equation has to be adapted with a slant angle).
- Range: The geometrical distance to P on the surface is
equal to the speed of light times the range time.
- Ellipsoid: Force the point to lie on an ellipsoid.
The equations for the point P on the ellipsoid and the satellite S in
its orbit are (where x denotes (x,y,z)):
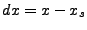 |
(D43) |
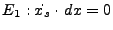 |
(D44) |
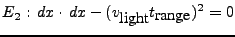 |
(D45) |
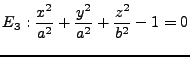 |
(D46) |
To compute the coordinates of a point P on the ellipsoid,
corresponding with line l and pixel p in the master image
the following has to be done. First the position of the satellite has
to be computed (assumed exact) based on the line number and PRF (l to
azimuth time to interpolated position), and the velocities for this
time (by interpolation). Also the range time corresponding to the
pixel number is computed (based on RSR, assumed exact).
Next the set of equations is used to solve for P(x,y,z). This is done
iteratively by linearization, which requires the derivative of the
equations to x and approximate values for the unknowns (the
coordinates of the center (
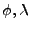 ) given in the SLC leader
file, converted to xyz on a sphere).
) given in the SLC leader
file, converted to xyz on a sphere).
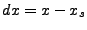 |
(D47) |
![$\displaystyle \left[ \begin{array}{lll} {{\delta E_{1}} \over {\delta x}} & {{\...
...r {a^{2}}} & {{2y} \over {a^{2}}} & {{2z} \over {b^{2}}} \\ \end{array} \right]$](img613.gif) |
(D48) |
Solving this exactly determined system of 3 equations yields the next
solution 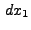 and the new values for the unknowns become
and the new values for the unknowns become
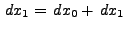 which are used to compute
which are used to compute 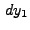 and
and 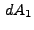 . The
solution is updated until convergence (
. The
solution is updated until convergence (
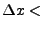 1e-6 meters).
1e-6 meters).
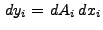 |
(D49) |
Where:
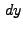 contains the observations. (set of equations)
contains the observations. (set of equations)
 contains the unknowns (coordinates of P).
contains the unknowns (coordinates of P).
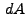 contains the partials (evaluated for previous solution).
contains the partials (evaluated for previous solution).
To solve for the azimuth time if the coordinates of a point on the
ground is known, only the Doppler D.45 equation needs to
be used. the derivative with respect to azimuth time of this equation
equals
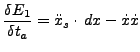 |
(D50) |
The solution is equal to (use approximate solution  to evaluate these expressions).
to evaluate these expressions).
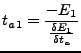 |
(D51) |
and
 |
(D52) |
The solution is updated until convergence (
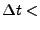 1e-10 seconds).
1e-10 seconds).
The range time is then computed as in equation D.46
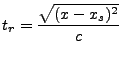 |
(D53) |



Next: Orbit interpolation
Up: Definitions
Previous: pixel number
Contents
Leijen
2009-04-14
![]() ) given in the SLC leader
file, converted to xyz on a sphere).
) given in the SLC leader
file, converted to xyz on a sphere).
![$\displaystyle \left[ \begin{array}{lll} {{\delta E_{1}} \over {\delta x}} & {{\...
...r {a^{2}}} & {{2y} \over {a^{2}}} & {{2z} \over {b^{2}}} \\ \end{array} \right]$](img613.gif)