Implementation

The observation equations are given by the zero-degree polynomial model (y = A x):

$$\left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_N \\ \end{array... ...array} \right] \left[ \begin{array}{c} \alpha_{l=0, p=0} \\ \end{array} \right]$$ (R1)

Where:
y contains the observed offsets in a certain direction.
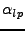$\alpha_{lp}$ denotes the unknown coefficients of the polynomial.

The least squares parameter solution is given by:

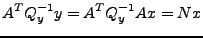$$A^T Q_y^{-1} y = A^T Q_y^{-1} A x = N x$$ (R2)

Where:
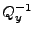$Q_y^{-1}$ is the (diagonal) covariance matrix of the observations.

The coefficients are estimated by factorization of the matrix N.

The inverse of matrix N is also computed to check the solution (stability) and to compute some statistics.

A check number is given ( 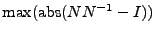${\rm\max(abs(}N N^{-1} - I))$) that gives a hint on the stability of the solution.