


Next: Method: adaptive
Up: Implementation
Previous: Implementation
Contents
The frequency shift 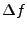 between the master and slave range data
spectra equals
between the master and slave range data
spectra equals
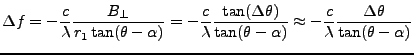 |
(V1) |
Where:
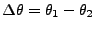 ,
, 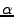 is the local terrain
slope w.r.t. the ellipsoid,
is the local terrain
slope w.r.t. the ellipsoid, 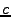 is the speed of light,
is the speed of light, 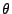 is the
local incidence angle (!),
is the
local incidence angle (!), 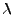 is the radar wavelength,
is the radar wavelength, 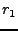 is
the slant range ground to master. The approximation is used in Doris.
Of course, the sign of
is
the slant range ground to master. The approximation is used in Doris.
Of course, the sign of
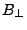 , or
, or
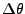 is important to
filter the correct side of the spectra. Note that
is important to
filter the correct side of the spectra. Note that
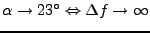 |
(V2) |
The local incidence angle is computed with the dot product of vectors
P, and P-M. See also [5].
The algorithm in Doris works as
- While there is a line in the overlap,
get next line for master and slave.
- Get block of FFT_LENGTH pixels.
- Compute viewing angle, perpendicular baseline, delta theta
for middle pixel of block.
- Compute frequency shift by equation 22.1,
and compose filter of rect and hamming.
- Filter master and slave.
- Write block back (for last block only partially).



Next: Method: adaptive
Up: Implementation
Previous: Implementation
Contents
Leijen
2009-04-14
![]() between the master and slave range data
spectra equals
between the master and slave range data
spectra equals
![]() ,
, ![]() is the local terrain
slope w.r.t. the ellipsoid,
is the local terrain
slope w.r.t. the ellipsoid, ![]() is the speed of light,
is the speed of light, ![]() is the
local incidence angle (!),
is the
local incidence angle (!), ![]() is the radar wavelength,
is the radar wavelength, ![]() is
the slant range ground to master. The approximation is used in Doris.
Of course, the sign of
is
the slant range ground to master. The approximation is used in Doris.
Of course, the sign of
![]() , or
, or
![]() is important to
filter the correct side of the spectra. Note that
is important to
filter the correct side of the spectra. Note that