The following analysis starts from the classical Fourier
domain description of interpolation errors in stationary signals.
Often these errors are quantified in terms of an L 
norm.
We will instead employ coherence theory for SAR interferograms
[1][2]
to predict the effect of interpolation on interferogram phase
quality.
Figure 1 shows (for the 1-D case) how the Fourier
transform I(f) of a
kernel i(x) acts as a transfer function on the periodically repeated signal
power spectral density 
.
The two classes of errors to be considered are: the distortion of the
useful spectral band 
, and the insufficient
suppression of its replicas 
,
where 
is the sampling frequency.
Hence, the interpolated signal will not be strictly lowpass limited and
the subsequent new sampling creates aliasing terms.
If in the resampling process all inter-pixel positions are equally
probable,
the aliasing terms are superposed incoherently and can be
treated as noise with a signal to noise ratio of:
In the following we will quantify interpolation errors in terms of
interferogram decorrelation and associated phase noise. We assume that
the original data 
has been sampled at least at the
Nyquist rate
and that the sampling distance after resampling is
similar to the original one.
Figure 1: Fourier transform I(f) of interpolator i(x) acting on the
replicated signal spectrum
The system model of figure 2 is sufficient for our analysis: consider a
perfect and noise free interferometric data pair of
coherence 
, before interpolation. Both and 
have passed
the SAR imaging and
processing system described by a transfer function H(f). Signal
additionally suffers from the interpolation transfer function I(f),
and alias noise n. It can be derived from [1] and
[2]
that for circular
Gaussian signals (i.e. for distributed targets)
the coherence of such a system is given by
These equations are readily extended to two dimensions. If both 
and 
are separable, we find:
The phase noise resulting from 
is known to be (in the
N-Look case):
where
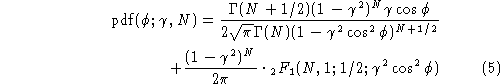
and 
is the Hypergeometric function.
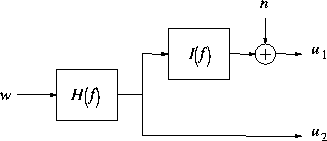
Figure 2: System model for evaluating interpolation errors (w is a
white circular Gaussian process)
