


Next: Algorithm
Up: DINSAR
Previous: Output Description
Contents
See also [20].
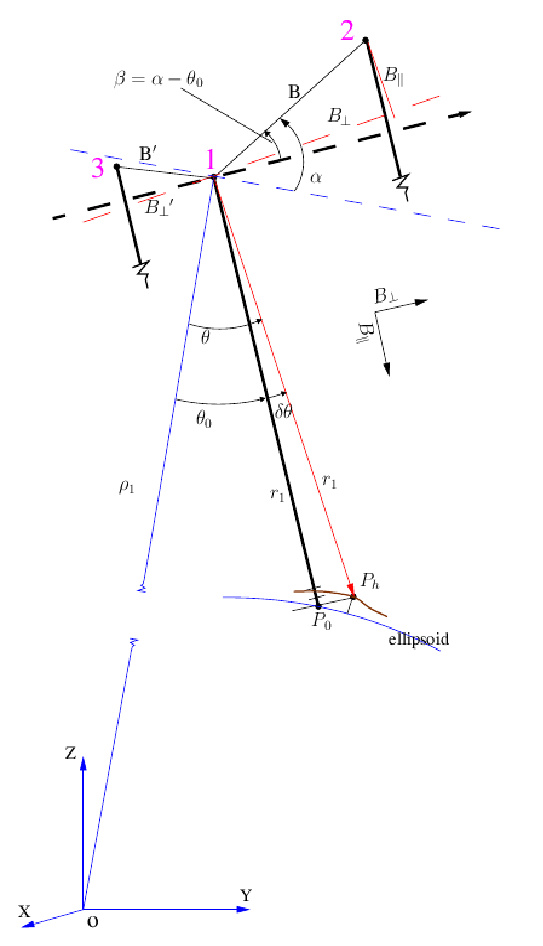
See figure 31.4
Simple equations for topo-pair (no deformation, no atmosphere, no other errors,
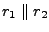 )
)
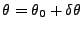 |
(1) |
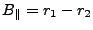 |
(2) |
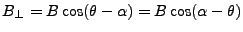 |
(3) |
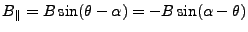 |
(4) |
The baseline components, for points on the reference ellipsoid (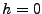 )
are
)
are
![$\displaystyle {\left[{B_{\perp}}\right]}_{h=0} = {B_{{\perp0}}}= B\cos(\theta_0-\alpha)$](img416.gif) |
(5) |
![$\displaystyle {\left[{B_{\parallel}}\right]}_{h=0} = {B_{{\parallel0}}}= B\sin(\theta_0-\alpha)$](img417.gif) |
(6) |
The 'true' phase of the interferogram is
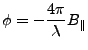 |
(7) |
And corrected for the phase of the reference body
 |
(8) |
For the defo-pair (1,3), denoted with a prime, similar equations
follow. Deformation in the line of sight (range), that occurred in
between the acquisitions, is denoted by 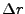
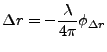 |
(9) |
A positive 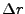 implies deformation in the
implies deformation in the
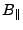 direction
(away from the sensor, i.e., subsidence). The phase of this
interferogram is
direction
(away from the sensor, i.e., subsidence). The phase of this
interferogram is
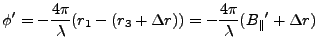 |
(10) |
Combining the expressions for the interferometric phase for the
topo-pair (31.7) and defo-pair (31.10)
yields:
 |
(11) |
The problem here is that the 'true' parallel baselines are unknown.
The (actually wrapped) phase of the deformation interferogram,
corrected for reference phase, is defined as:
where
 . Using the approximation for small
. Using the approximation for small
 (which is about
(which is about  or 0.0175 rad for terrain
height differences of 5 km)
or 0.0175 rad for terrain
height differences of 5 km)
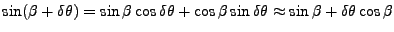 |
(13) |
it follows from equation 31.13 that the 'flat earth'
corrected phase equals
The corrected phase for the topo pair equals
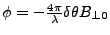 (using the same approximation),
and combining this with 31.15 yields
(for the 'flat earth' corrected phases)
(using the same approximation),
and combining this with 31.15 yields
(for the 'flat earth' corrected phases)
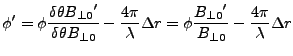 |
(15) |
or
![$\displaystyle \Delta r = -\frac{\lambda}{4\pi} [\phi' - \phi \frac{{B_{{\perp0}}}'}{{B_{{\perp0}}}}]$](img436.gif) |
(16) |
or for the phase
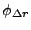 caused by the deformation
caused by the deformation 
 |
(17) |
This important equation shows how to obtain offset vectors from 3 SLC
images, i.e., by scaling the (reference phase corrected) unwrapped
phase of the topo-pair by the ratio of the perpendicular baselines (to
points on reference body), and subtracting this from the phase of the
defo-pair. This can thus be performed without the 'true' values for
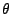 are required.
are required.
Figure 31.4:
Geometric configuration for 3-pass differential insar. The
orbits go 'into' the paper. All angles are defined
counterclockwise. The terrain element 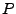 corresponding to the
radar coordinate (l,p) is located at a height
corresponding to the
radar coordinate (l,p) is located at a height 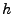 above the
ellipsoid. The perpendicular baseline required for this method is
the one for points
above the
ellipsoid. The perpendicular baseline required for this method is
the one for points 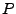 located on the reference ellipsoid (
located on the reference ellipsoid (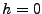 ).
).
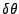 , the change in
, the change in 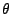 since
since 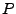 is on a height
is on a height 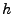 ,
due to a 5 km height difference, is approximately
,
due to a 5 km height difference, is approximately 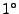 .
.
 |
Subsections



Next: Algorithm
Up: DINSAR
Previous: Output Description
Contents
Leijen
2009-04-14
![]() )
)

![]()
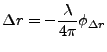

![$\displaystyle \Delta r = -\frac{\lambda}{4\pi} [\phi' - \phi \frac{{B_{{\perp0}}}'}{{B_{{\perp0}}}}]$](img436.gif)
